


But it is not so clear how to ensure that just for every even very huge number, it is always possible. We can check that it is possible for one, for two, for three, for four, and so on.
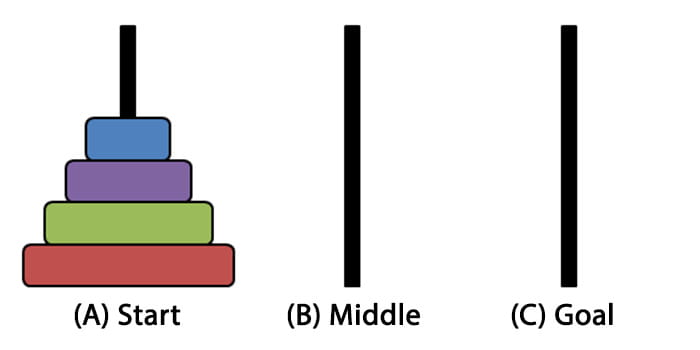
At the same time, it is not clear at this point how can we be sure that it is possible for every possible value of n. First of all, we are allowed to move only one disc at a time, and naturally we need to take the top most disc from one stick, and to put it to some other stick, right? And also we are not allowed to put a larger disc onto a smaller disc, okay? So the question is whether it is possible for, and if it is possible, then for which values of n this is possible, okay? So it is known to be possible for every value of n. This would be easy if not given two constraints. Our goal is to move all n discs to some other stick, to one of the two empty sticks. On the first stick, we have n discs, sorted by size as shown here on the slide. In this puzzle, we're given three sticks. Our final example is the well known Hanoi Towers puzzle. Basic programming knowledge is necessary as some quizzes require programming in Python. We assume only basic math (e.g., we expect you to know what is a square or how to add fractions), common sense and curiosity.Ģ. In the online course, we use a try-this-before-we-explain-everything approach: you will be solving many interactive (and mobile friendly) puzzles that were carefully designed to allow you to invent many of the important ideas and concepts yourself.ġ. We will use these tools to answer typical programming questions like: How can we be certain a solution exists? Am I sure my program computes the optimal answer? Do each of these objects meet the given requirements? In this course, we will learn the most important tools used in discrete mathematics: induction, recursion, logic, invariants, examples, optimality. Mathematical thinking is crucial in all areas of computer science: algorithms, bioinformatics, computer graphics, data science, machine learning, etc.


 0 kommentar(er)
0 kommentar(er)
